这个87.53%已经被证实只是个玩笑。在众多（只顾怀疑、相互抄袭、转载、或来路不明的）博客文章中，段炼的角度显然和所有人都不一样，他把所有的百分比数据的搜索频数都下载了下来，大家一看就知道，87.53这个数字本身并没有什么奇怪的，你去搜87.52或87.54都一样。众人纷纷解释这个0.53（100人中哪里来的0.53个人），不知道谁第一个提起了置信区间，总之我刚才看到的杯具有（考虑了一下，不是啥好事，就不给链接了）：
……在计算样本容量的时候要考虑一个置信区间的问题，也就是说调查了100个人，但是并不认为这100个人都是认真作答的，因此会在样本容量上再乘上一个置信度。
置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。
第一种说法简直错了十万八千里，我闻所未闻，真是木有想到，置信度原来还有这种功效；第二种说法是对置信区间常见的误解；我正欲吐血时，竟然看见了维基百科的身影：置信区间。这下是真的杯具了，维基上赫然写着：
置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。
显然这句话极富误导性（此处不谈贝叶斯学派的观点），还好该页面底下的理论部分是正确的。杯具继续：
通常很少计算某个统计量的点估计值，而是在控制两类错误的条件下，计算它的估计区间的上下界。例如我们可以用90%的概率推断，比率落在81.47%~87.53%中（只是描述问题，并无数据依据），然后有时会根据问题背景，将估计值用区间上界或下界表示。在本案例中，0.53们认为“支持”是他们想要的结果，不排除取上界的可能。
这种冠冕堂皇的话恐怕是领导最喜欢了，什么两类错误啊（Type I & Type II），什么上界下界啊，寡人用名词堆死你。首先，在绝大多数情况下，第二类错误是无法控制的（如备择假设不明确、真实effect size不知道），能知道的只有第一类错误的概率；其次，历史上就没有过用一个置信区间的上界或下界作为估计值的，要么给区间估计，要么给点估计，要是估计值可以随便取，那统计学真的是个大杯具，本来大家只是不相信统计数据，这么整下去总有一天统计理论与方法也会被糟蹋得不像样子的（其实已经被糟蹋得够可以了）。
还有人搬出比率估计啊抽样啊来解释，看着相当的神秘，但问题就是，这个问题本来就不是问题。大家摸象摸到了左前腿，心想世上怎么有这么大一条腿，于是开始解释它，可是还有另外三条腿都很大啊……
总结一点：世上的争论多因观测局部样本引起。
我对段炼的数据倒是挺感兴趣，这是另一个主题，我还没考虑好，打算改天写到统计之都上去。先简单放两幅图，以搜索gov.cn中的百分比为例。首先是每个百分比对应的频数：
gov.cn中每个百分比对应的搜索频数
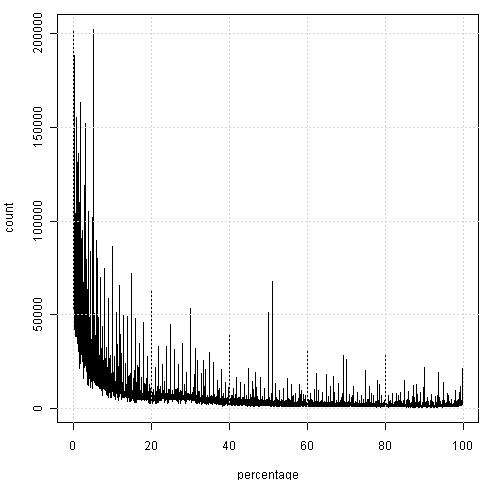
我们能看到，这图中有些“毛刺儿”，显然容易想到，可能是某些“整数位”上的百分比会偏高，那么“放大”一下看看局部吧：
在长度为1的区间内看搜索频数
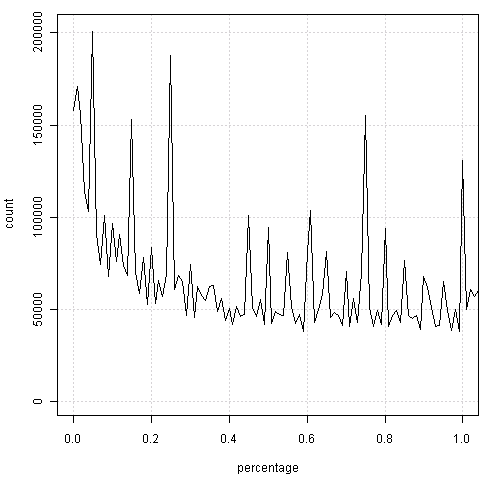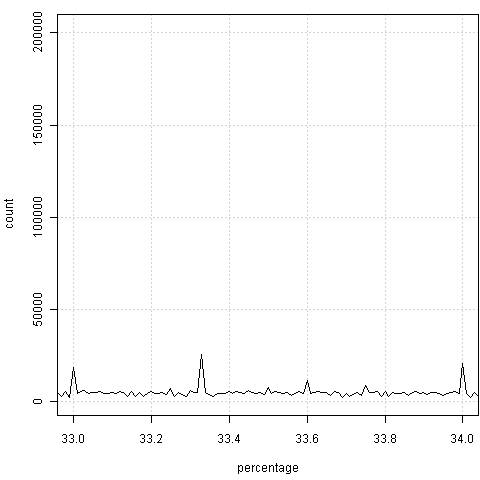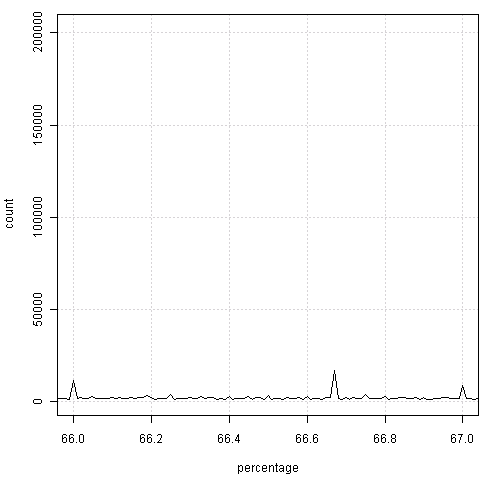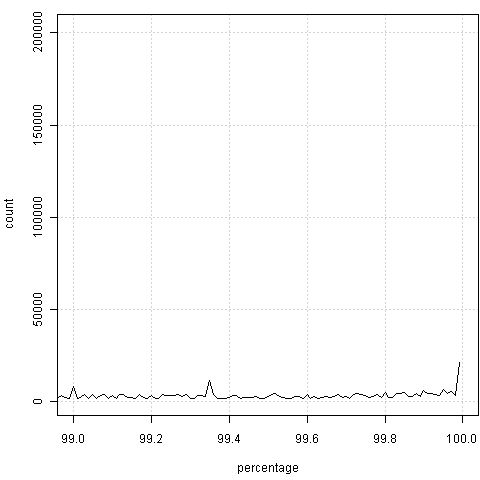
如果视力没问题的话，很容易感觉到两边总是会出现“凸起”——也就是整数百分比上的频数会偏高。原因是什么，我不知道，也许是官员秘书们习惯不保留小数。
再简单用LOWESS验证一下在整数位和不在整数位上的频数是否有显著差异，由于频数数据本身数量级很大，所以纵坐标取了对数，这图的形状看起来和第一幅图有所不同：
整数百分比xx.00%上的频数
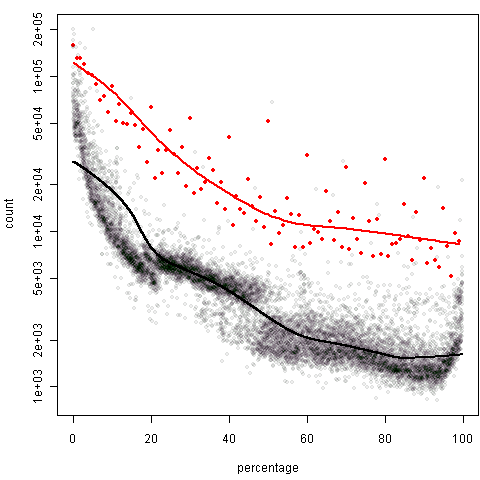
这种图可以和协方差分析的思想结合起来看，即：控制了百分比这个变量之后，在整数位和不在整数位上频数的差异如何。两条平滑曲线有明显的高低之分，所以取整的效果还是很明显的。继续看xx.x0%这种取整方式：
取整为xx.x0%形式的百分比上对应的频数
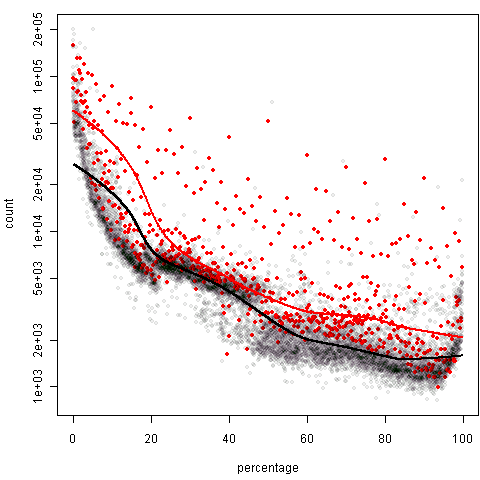
它不如上一种取整方式的区别明显，但总的来说，取整和不取整的差异都是很显著的。我试了试直接用回归（协方差分析），发现实在是太难调自变量的阶数了，一元回归肯定是不行，残差图奇形怪状，压根儿就不会是线性关系。
以上都不应该是分析的关键，只是说明一下探索的可能性。真正好玩的应该是这种百分比的频数究竟应该服从什么分布，我也不知道，但至少可以把我天朝的百分比和别的网站的百分比数据做个卡方检验，看分布是否吻合，也就是说，天朝使用百分比的习惯和别人是否有显著差异。
感谢段炼在个人网站中提供了数据下载，使得本文的结果具有可重复：
## 如果段炼不删掉这个数据的话，以下分析可重复
x = read.table("http://chemhack.com/data/googleNums/gov.cn.txt",
sep = ",", col.names = c("percentage", "count"))
x$round0 = x$percentage %in% seq(0, 100, 1)
x$round1 = x$percentage %in% seq(0, 100, 0.1)
plot(count ~ percentage, x, type = "l")
grid()
library(animation)
saveMovie({
for (i in 0:99) {
plot(count ~ percentage, x, type = "l", xlim = i + c(0,
1), panel.first = grid())
}
}, interval = 0.5, moviename = "percent-count", para = list(mar = c(4.5,
4, 1, 0.1)))
plot(count ~ percentage, x, pch = 20, col = rgb(0:1,
0, 0, c(0.07, 1))[x$round0 + 1], log = "y")
lines(lowess(x[x$round0, 1:2], f = 1/3), col = "red", lwd = 2)
lines(lowess(x[!x$round0, 1:2], f = 1/3), col = "black", lwd = 2)
plot(count ~ percentage, x, pch = 20, col = rgb(0:1,
0, 0, c(0.07, 1))[x$round1 + 1], log = "y")
lines(lowess(x[x$round1, 1:2], f = 1/3), col = "red", lwd = 2)
lines(lowess(x[!x$round1, 1:2], f = 1/3), col = "black", lwd = 2)
本文也算是相应JD同学的号召，从长时间的Keep on Eating回到正道上。
又是一篇好文章啊，特别是那个动画很有感觉。
为了显露我无聊的本性，挑两个小刺吧……
一是第4个blockquote下面第三行的“能知道的只有第一类错误的概率”，应该是“能控制的只有第一类错误的概率”。
二是最后一幅图下面第二行的“是在”应该是“实在”、
谢谢纠正错别字。
你觉得第一类错误的概率能控制么？我觉得这个概率本来就是可以计算的，它不受人控制。人能知道的就是如果拒绝零假设，犯错误的概率是多大，从而决定要不要拒绝零假设。（成了个语文问题？……）
我是这样想的，在一类假设检验问题中，原假设并没有给出参数的一个确定的值，而是一个范围，比如有了一个服从
的样本
，我要检验
，这个时候计算犯第一类错误的概率
拒绝原假设
，很显然只要
没有确定的值 ，这个概率就无法计算。但是我们知道，如果原假设为真的话，那么这个概率是随着
的增大而递减的，也就是说我犯错的可能性最大是在
的时候，如果我把
时的错误都限定在一个很小的水平上，那么就更不用说
的情形了。
所以我的想法是有些情况下第一类错误的概率是无法精确“知道”的，但如果我们把其上界限定好了，那么就相当于“控制”住了第一类错误。
可能这里我用词不当吧。
如果“这个概率”用积分式来表示的话，“很显然”、“我们知道”这些用语就更容易理解了。
OK，“控制”的意思就是在零假设为不确定数值的情况下，得到的是P值的上界。好吧，那我的“知道”就理解为“了解”好了，而不是确切知道
LaTeX公式是我改的，这里的插件和COS中用的插件是一样的，可以用$latex $写公式。
其实都是一个意思，是我有点钻牛角尖了。
哇，居然自动支持LaTeX公式，我记得我没加任何标签啊，还是师兄帮我改的？:)
刚看两幅LOWESS图，突然吓一跳，心想原图是纵坐标取了对数的，而
lines()没有指明对纵坐标取对数，这两条线是不是不对啊。回头一看?par，发现这些作图函数是会自动处理对数问题的，当plot()中用了log = "y"之后，参数par("ylog")就变成TRUE了，以后的作图函数都会根据这个参数相应调整坐标系。嗯，没搞错。这?par真是一辈子看不完、记不住啊。生平第一次自己回复自己的文章……
依稀记得老大说过某寒假用了整整三天的时间来学习par()……
是的，那算是统计图形的书的“导火索”之一。
R图形的灵活性对一些用户来说也是灾难啊，确实是什么都能定制，但学起来也太费劲了，不过no pain no gain，世上也没那么多捷径可走。
yihui对图形真是精益求精啊！我们只要整个大差不差就可以了，统计要学的实在太多啊。
我一直是这个观点，街头随便找100个人根本就不算是概率抽样，后面的置信区间,bootstrap之类的根本就无从谈起。
如果去分析一下统计年鉴的数据，你会发现更杯具的，中国的经济增长数据基本是完美指数型、变量关系是（散点图）完全直线型。