Coin-flipping is a rather old topic in probability theory, so most of us think we know very well about it, however, the other day I saw a question about this old topic (in David Smith’s REvolution?) which was beyond me expectation: how many times do we need to flip the coin until we get a sequence of HTH and HTT respectively? (For example, for the sequence HHTH, the number for HTH to appear is 4, and in THTHTT, the number for HTT is 6.)
It seems that the two results are equivalent, as H and T occurs with equal probability 0.5, so we naturally believe the average numbers of steps to HTH and HTT are the same, but the fact is not as we imagined.
## smart guys use math formulae to solve the problem,
## but *lazy* guys like me use simulations with R
coin_seq = function(v) {
x = rbinom(3, 1, 0.5) # sequence of coin results
n = 3 # a counter
while (!all(x == v)) {
x = c(x[-1], rbinom(1, 1, 0.5))
n = n + 1
}
n
}
set.seed(919)
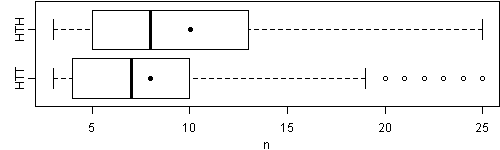
mean(htt <- replicate(1e+05, coin_seq(c(1, 0, 0))))
# [1] 8.00304
mean(hth <- replicate(1e+05, coin_seq(c(1, 0, 1))))
# [1] 10.0062
png("coin-htt-hth.png", height = 150, width = 500)
par(mar = c(3, 2.5, 0.1, 0), mgp = c(2, 0.8, 0))
boxplot(list(HTT = htt, HTH = hth), horizontal = T,
xlab = "n", ylim = range(boxplot(list(HTT = htt, HTH = hth),
plot = FALSE)$stats))
points(c(mean(htt), mean(hth)), 1:2, pch = 19)
dev.off()
The answer is counterintuitive, isn’t it?
Well, mathematicians certainly do not like my solution (I guess they even hate such an imprecise approach). I hope some smart guys can give me some hints on working out the probability distribution and hence the expectation.