如同经济学家不讲道德一样(学过经济学的人都知道这句话的意思),理论统计学家从某种程度上来说也不讲道德。我们常用的一些统计量通常都渐近服从某种分布(以卡方和正态为典型),看起来做理论的人对这些渐近理论都非常骄傲和自豪,我们在学习过程中也要一代一代传承下去。数学公式摆出来当然能唬人,也许唬到最后大家都为光着屁股的皇帝欢呼。坦白说,我对这些东西感到非常厌倦。
近日来收到邮件少了,但各个问题都不太好直接回答。比如这则关于McNemar检验的问题:McNemar检验可以有两种形式的统计量,一为 (b - c)2/(b + c),一为 2b*log(2b/(b+c)) + 2c*log(2c/(b+c)),其中b和c是列联表非对角线上的频数。前者是McNemar检验本身的统计量,可以根据渐近正态分布得来(然后平方得到卡方),后者是似然比统计量(不带约束的似然除以带约束的,取对数,乘2)。McNemar检验看似复杂,实际上可以简化为检验b = c,或等价于检验一个n = b+c的二项分布中,是否p = 1/2(观察到X = b或c)。现在的问题是,这两种统计量有没有优劣之分?
作为一个懒得推公式的人,我向来喜欢用模拟回答问题,因为模拟的结果非常直截了当。我的考虑是,要看渐近统计量的优劣,那就看随着n增大,统计量和渐近分布有多接近好了。一个自然而然的想法当然是对若干统计量的观测值做分布检验了,比如KS检验。我们知道这两个统计量都是自由度为1的卡方分布,剩下的事情就是计算:
set.seed(123)
nmax = 1000
p = matrix(nrow = nmax, ncol = 2)
for (n in 2:nmax) {
# 生成服从二项分布的随机数,分别计算两种统计量并作KS检验、记录P值
b = rbinom(500, n, 0.5)
x1 = (b - (n - b))^2/n
x2 = 2 * b * log(2 * b/n) + 2 * (n - b) * log(2 * (n - b)/n)
p[n, 1] = ks.test(x1, "pchisq", df = 1)$p.value
p[n, 2] = ks.test(x2, "pchisq", df = 1)$p.value
}
# 调整一下数据格式,画图:随着n增大,P值如何变化?
library(ggplot2)
d = melt(p, varnames = c("n", "method"))
d$method = factor(d$method, labels = c("McNemar", "LRT"))
colnames(d)[3] = "p.value"
qplot(n, p.value, data = d, shape = method, geom = c("smooth", "point")) +
scale_shape_manual(values = c(2, 3))
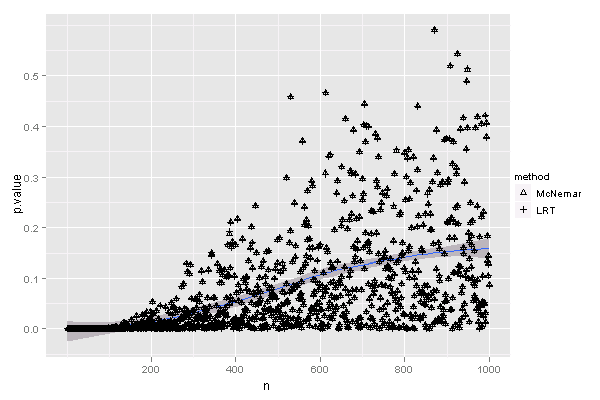
实际上,两种统计量与卡方分布的接近程度几乎是一样的,对于每一个n,KS检验得到的P值都差不多,可以看见图上两种方法检验得到的P值基本上是重叠的(其实也意味着统计量的值差不多),而n过了200之后,统计量基本上和卡方分布拟合比较好,即P值较大,但这种关系并不严格。
渐近理想国(asymptotia),来自Little (2006)在The American Statistician的文章,这词在英语词典中查不到,我将它翻译为“渐近理想国”。该文章是讲频率学派与贝叶斯学派的争论,提到人们对“渐近”的无奈:一个步履蹒跚的旅人,心想这理想国嘛时候才能到达呢?
至少在McNemar检验中,这个问题有了一个模糊的答案。