做统计的经常涉及到在分布函数或密度函数表示概率,例如将P(X<x)的区域涂色,这用多边形很容易办到。有人可能不理解,密度函数不是光滑的么,多边形的边不光滑,怎么能填充我们需要的区域?须知数学和现实往往有差距,数学中存在连续、光滑的概念,计算机中(目前)是无法精确表达这些概念的,而且很多情况下没有必要,例如图形中就没必要取遍一段区间上的所有实数再画图,这本来也是不可能的,因此只需要近似就够了。
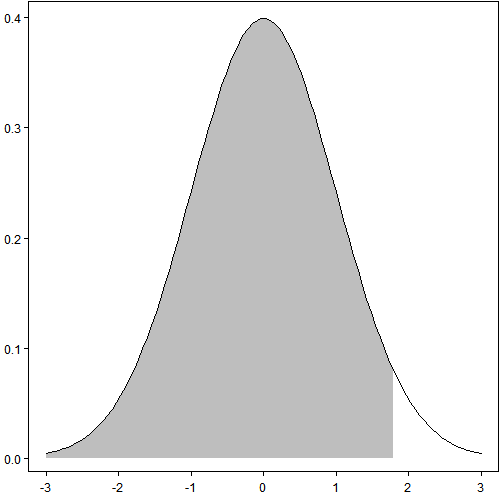
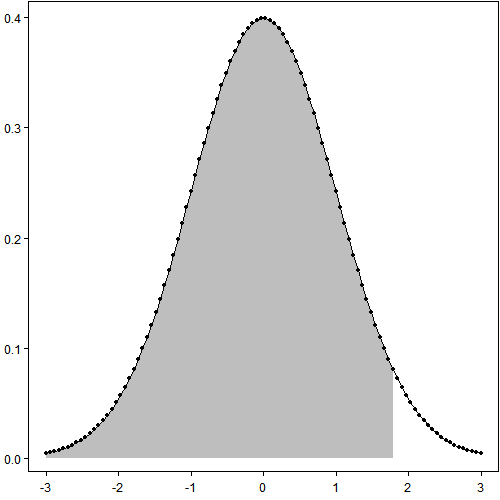
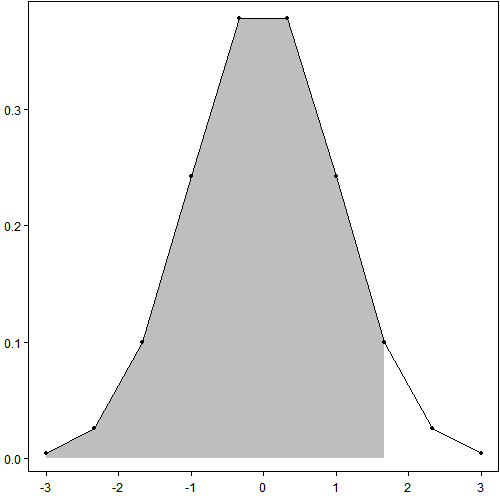
以下三幅图说明了这个近似的过程:第一幅图看起来很光滑很强大;第二幅图和第一幅图完全相同,只是把作图用到的数据点标了出来——实际上只用了[-3, 3]区间上的100个点;第三附图只用了10个点,图穷匕首见。
# png("polygon%d-s.png", width = 500, height = 500)
par(mar = c(2, 2, 0.1, 0.1), las = 1, mgp = c(3, 0.5, 0), tcl = -0.3)
x1 = seq(-3, 3, length = 100)
plot(x1, dnorm(x1), type = "n")
polygon(c(x1[1], x1[1:80], x1[80]), c(0, dnorm(x1[1:80]), 0), col = "gray", border = NA)
lines(x1, dnorm(x1))
plot(x1, dnorm(x1), type = "n")
polygon(c(x1[1], x1[1:80], x1[80]), c(0, dnorm(x1[1:80]), 0), col = "gray", border = NA)
lines(x1, dnorm(x1),type='o',pch=20)
x2 = seq(-3, 3, length = 10)
plot(x2, dnorm(x2), type = "n")
polygon(c(x2[1], x2[1:8], x2[8]), c(0, dnorm(x2[1:8]), 0), col = "gray", border = NA)
lines(x2, dnorm(x2),type='o',pch=20)
# dev.off()